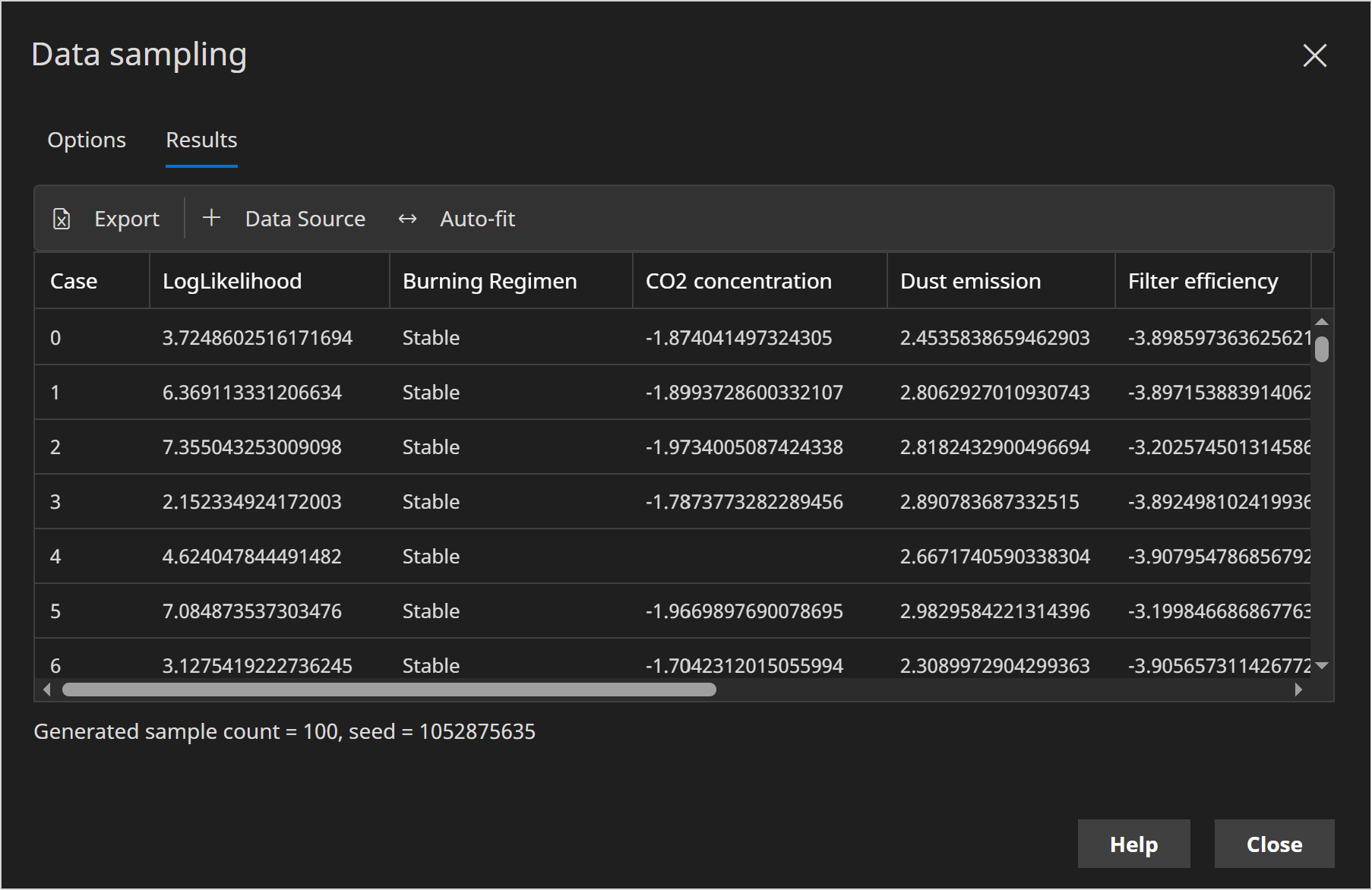
Data sampling

For a tutorial please see Data Sampling tutorial

Introduction

Data Sampling is the process of generating data from a Bayesian network or Dynamic Bayesian network. Some uses for Data Sampling are:

• Generating data to understand and visualize a network.
• Generating test data.
• Understanding how the log-likelihood varies.

info

We could delete all the distributions in the network and learn them from scratch from our sample data. With enough samples, the distributions will look very similar.

How does Data Sampling work?

For each record (case) we generate, we need to sample from each node's respective probability distribution.

Conditional probabilities

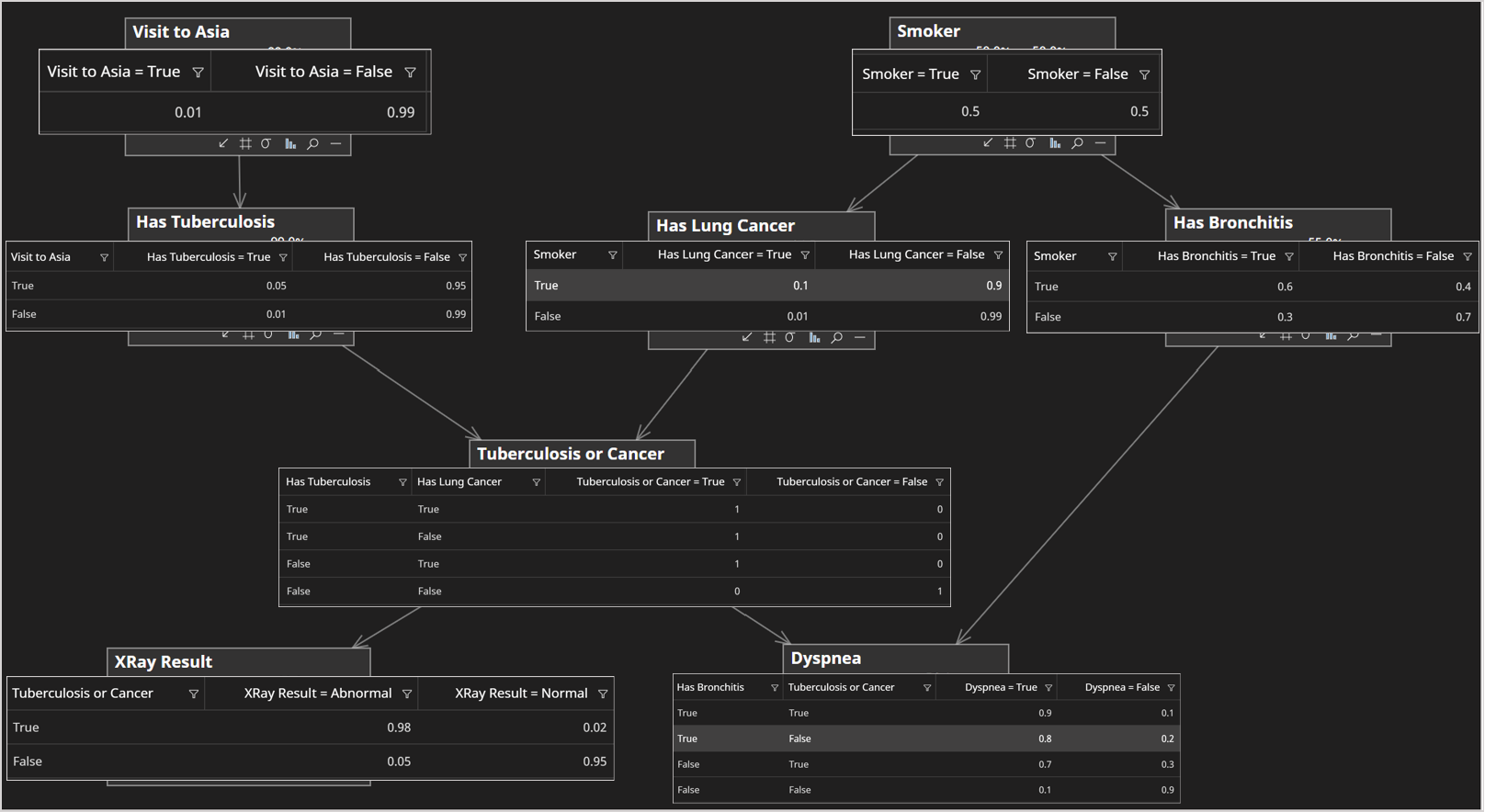
In a Bayesian network, each node requires a distribution conditional on its parents. For example, the image below shows the Asia network, with each distribution shown overlaid for each node.

The Visit To Asia node, only requires the distribution $P(\text{Visit to Asia})$ as it has no parents, whereas Has Lung Cancer requires the distribution $P(\text{Has Lung Cancer} | \text{Smoker})$.

Topological Sort

Sampling from the $P(\text{Visit to Asia})$ is simple. We can generate a number $x$ between 0 and 1. If $x < P(\text{Visit to Asia} = True)$ we can use True as our sampled value. However if we want to sample from Has Lung Cancer we first need a sample for Smoker so we can sample from $P(\text{Has Lung Cancer} | \text{Sampled value for Smoker})$.

This is where an algorithm called a Topological Sort comes in handy. It generates a linear sequence of nodes, such that any parent comes before its child in the sort.

An example for the Asia network is shown in the image below.

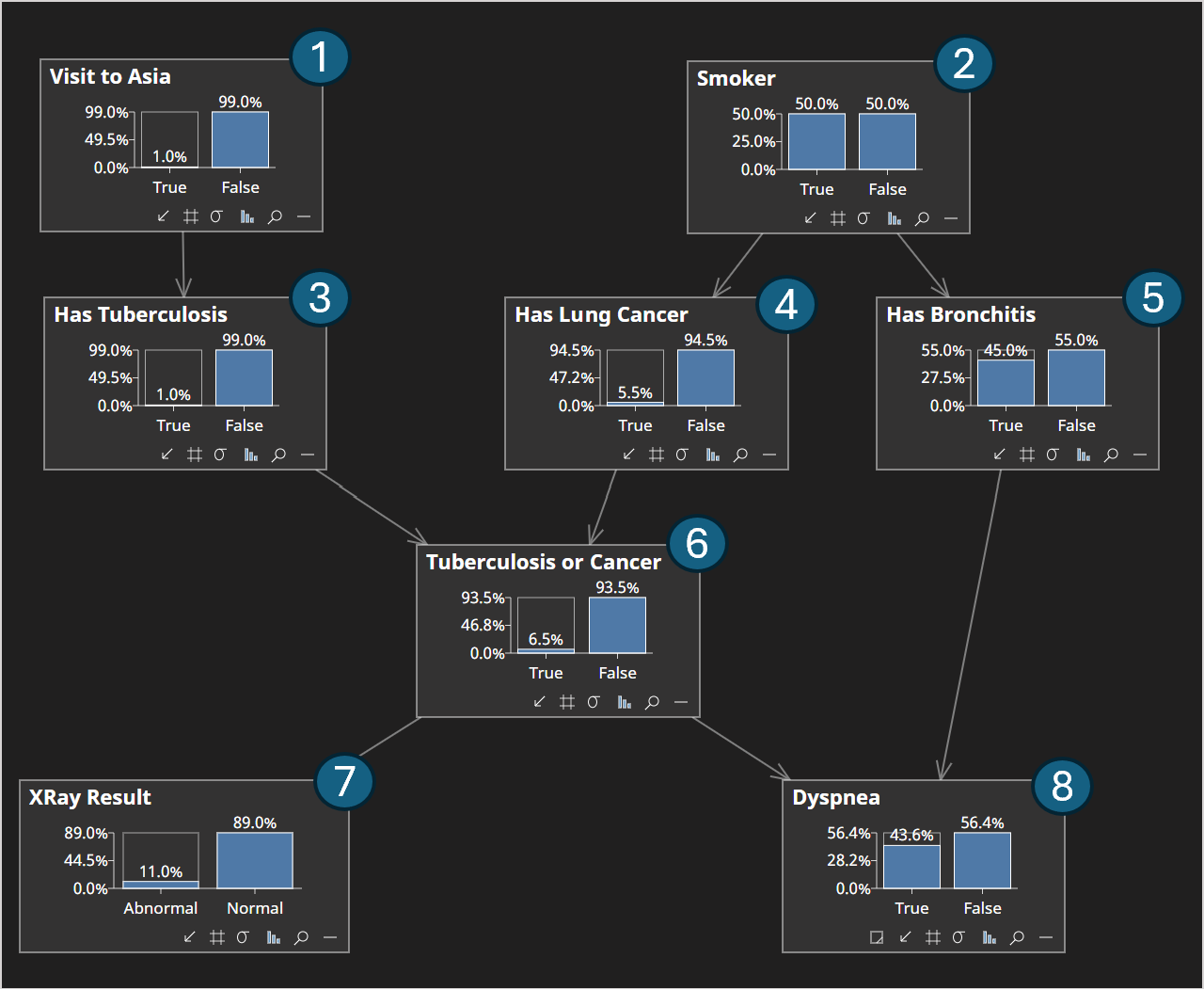
By sampling using this sort, we can ensure that whenever we come to sample from a node, we always have samples for its parents.

Log Likelihood

When the Log Likelihood option is true, an additional column is added to the sampled data, which reports the Log likelihood of the generated sample.

note

When evidence is fixed, each case has an associated weight that can be output if necessary. The log-likelihood output however is unweighted. i.e. it reflects the log-likelihood of the case as if it had a weight of 1.

Weight / Log(weight)

Bayes Server supports sampling data when certain evidence is fixed. When evidence is fixed, each sample has an associated weight, which is the likelihood of the fixed evidence for the current sample. This indicates how likely it is that the fixed evidence could have occurred with this sample.

To output the weight, ensure the Weight options is true or the Log Weight options is true.

info

When we have fixed evidence, the weight is important as it ensures our generated data is representative of the overall distribution of the network. As mentioned earlier, we could use the samples to learn the network distributions from scratch and with enough samples, they will look similar. However if you learn the parameters without the Weight they will not. Equally if you are using the samples in a downstream application or code, it is important to use this weight.

Calculation

The weight is calculated as follows:

• For each sample generated, it is initialized to 1.
  • If you have no fixed evidence, all samples will have a weight of 1.
• Then, as per the topological sort described earlier, when you reach a node $X$ that has fixed evidence, you pick the subset of the distribution that corresponds to the sample values for the parents in the normal way, leaving you with $P(X)'$.
• Rather than sampling, we use the fixed evidence value for $X$
• We then need to multiply the weight by the associated probability for the fixed value in $P(X)'$.

info

Log weight is useful when the likelihood of the fixed evidence can be very small, such as when sampling from time series and sequences. The log weight is simply log(weight) however is calculated in such a way that it does not suffer from underflow problems.

Current Evidence

When the Current Evidence option is true, any evidence currently entered in the current Bayesian network or Dynamic Bayesian network will be used in the data sampling process.

Missing Data

By specifying a value between 0 and 1 (inclusive), in the missing data Probability text box, a proportion of values will be randomly set to missing (null/unobserved). Optionally an additional minimum probability can be specified in the Probability (Min) text box. When set, the missing data probability for each case varies randomly between the two specified probabilities.

info

The missing data mechanism used is Missing Completely At Random (MCAR).

Export

Data can be easily exported.

For example, this is useful to understand how the log-likelihood varies.

DBN Sampling

When sampling from networks with DBN variables (Dynamic Bayesian networks), the sample count does not equal the number of sequence rows generated, but rather the number of cases generated, each of which will have its own sequence.