Log likelihood
For a tutorial please see Log Likelihood tutorial.
Introduction
When evidence is entered in a Bayesian network or Dynamic Bayesian network, the Probability (likelihood)
of that evidence, denoted P(e) can be calculated.
The Probability of evidence P(e) indicates how likely it is that
the network could have generated that data. The lower the value, the less likely.
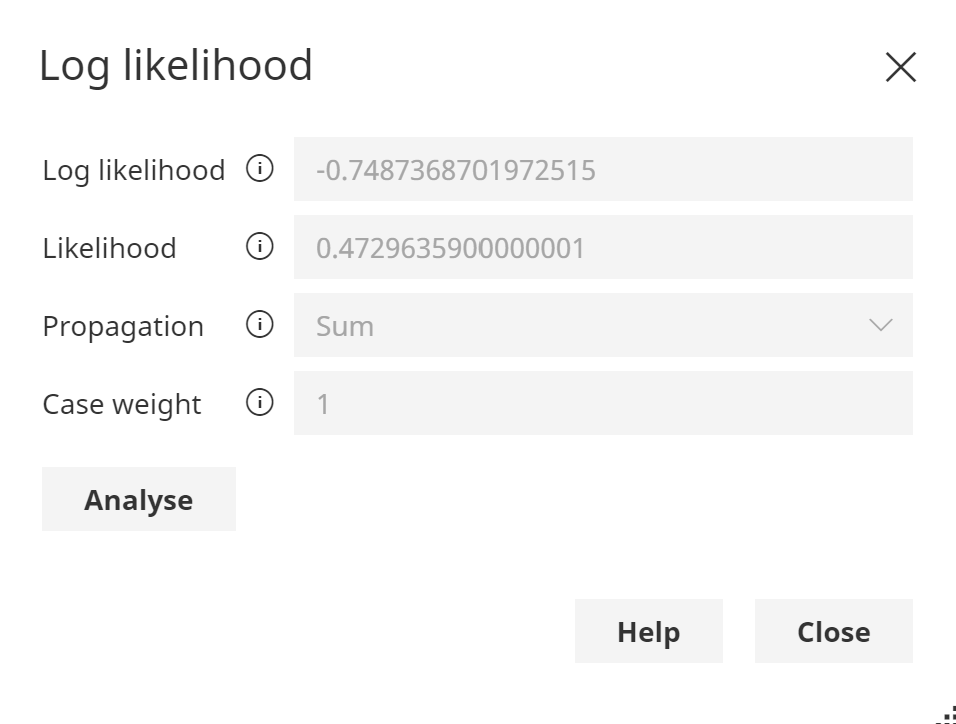
Log value
The Log Likelihood Log(P(e)) is also reported, as the P(e) can often report zero, due to underflow caused by the repeated multiplication of small probability values, using floating point arithmetic.
Bayes Server uses sophisticated algorithms to detect very small log-likelihood values
An example of zero likelihood:
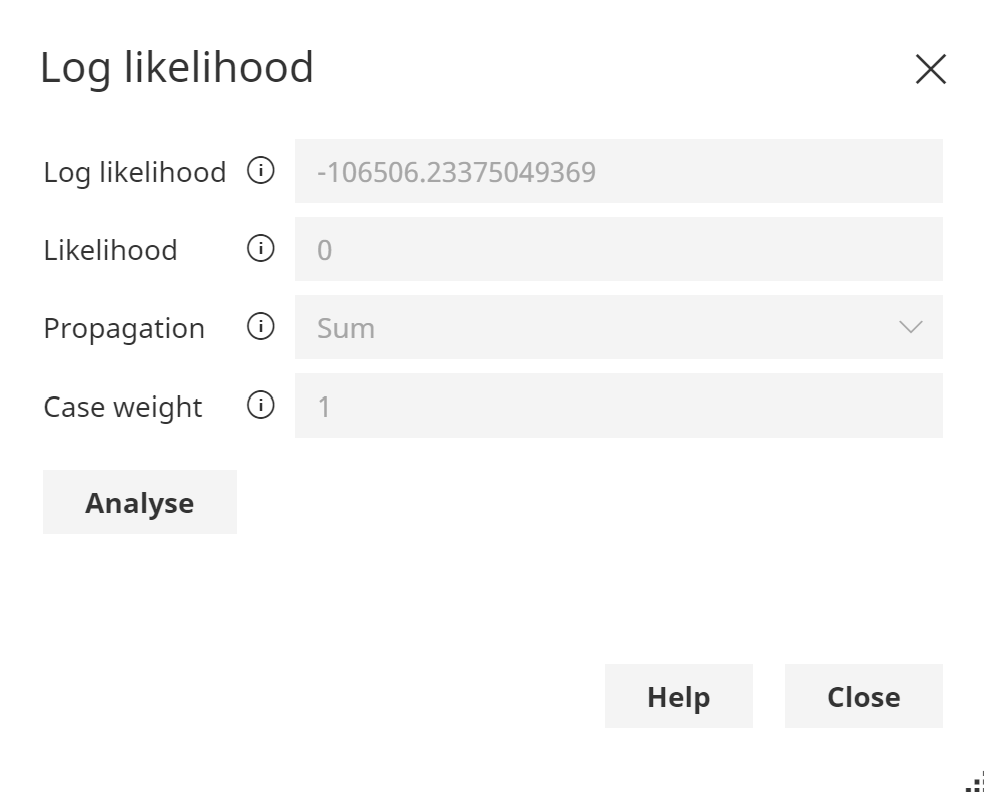
Log Likelihood values are often used to detect unusual data, known as Anomaly detection.
Range of values
The likelihood P(e) in networks with only discrete nodes lies in the range [0, 1], therefore the log-likelihood lies in the range [-Infinity, 0]. For networks that contain one or more continuous nodes (with or without discrete nodes) the likelihood (pdf) lies in the range [0, +Infinity], therefore the log-likelihood lies in the range [-Infinity, +Infinity].
Log-likelihood -> Probability
While log-likelihood values from the same model can be easily compared, the absolute value of a log-likelihood is somewhat arbitrary and model dependent. The HistogramDensity class in the API can be used to build a distribution of Log-Likelihood values for a model which can then be used to convert log-likelihood values to a value in the range [0,1].
This techniques is often used in anomaly detection applications when we wish to report the health of a system as a single meaningful value.
Log-likelihood (Most probable)
When Most probable explanation (MPE) is used, the log-likelihood/likelihood is the same value you would get if you were to calculate it without Most Probable explanation on, but having evidence set according to the most probable configuration.