Structural learning
Structural learning
Structural learning is the process of using data to learn the links of a Bayesian network or Dynamic Bayesian network.
Bayes Server supports the following algorithms for structural learning:
- Clustering
- PC
- Search & Score
- Hierarchical
- Chow-Liu
- Tree augmented Naive Bayes (TAN)
You can chain algorithms together (e.g. Search & Score + Clustering). Simply finish the structural learning wizard multiple times, each time importing link constraints from a previous run.
Clustering
(since version 8.4)
Automatically determines an appropriate discrete latent variable to add to the model, which can model hidden patterns. Similar to a cluster model or a mixture model. Supports networks with discrete and/or continuous variables, as well as missing data.
See our article on mixture models & clustering for more information.
This is an unsupervised algorithm, and in its most basic form is similar to a mixture model (a.k.a. cluster model). However this algorithm is more flexible, as an arbitrary structure can be mixed, and include both discrete and continuous variables. The appropriate number of clusters is automatically determined by the algorithm robustly using cross validation.
PC algorithm
A constraint based algorithm, which uses marginal and conditional independence tests to determine the structure of the network.
This algorithm supports the following:
- Learning with discrete and continuous variables, including hybrid networks with a mixture of discrete and continuous.
- Learning both Bayesian networks and Dynamic Bayesian networks. (e.g. Learning from Time Series or sequence data).
- Learning with missing data (discrete or continuous).
The algorithm does not currently support the automatic detection of latent variables.
References:
An algorithm for fast recovery of sparse causal graphs | P Spirtes, C Glymour - Social science computer review, 1991
Causation, prediction, and search. Adaptive computation and machine learning | P Spirtes, C Glymour, R Scheines - 2000 - MIT Press, Cambridge
Significance level
The significance level is used during tests for independence and conditional independence by the algorithm to determine whether links should exist or not. A value of 0.05 or 0.01 is typical.
Max conditional
This controls the number of conditional nodes that are considered when the algorithm performs conditional independence tests.
A value of 3 means that when testing whether X and Y are independent, up to 3 other conditional variables will be considered in the tests.
Max temporal
This is the maximum order that should be considered for temporal links in dynamic Bayesian networks.
A value of 3 means that temporal nodes should not have links greater than order 3, i.e. up to 3 previous time steps.
Search & score algorithm
(since version 7.14)
The Search & Score algorithm performs a search of possible Bayesian network structures, and scores each to determine the best.
This algorithm currently supports the following:
- Discrete variables.
- Continuous variables.
- Hybrid networks with both discrete ad continuous variables.
- Learning with missing data.
References:
A Bayesian method for the induction of probabilistic networks from data | GF Cooper, E Herskovits - Machine learning, 1992
A tutorial on learning with Bayesian networks | D Heckerman - Learning in graphical models, 1998
Optimal structure identification with greedy search | DM Chickering - Journal of machine learning research, 2002
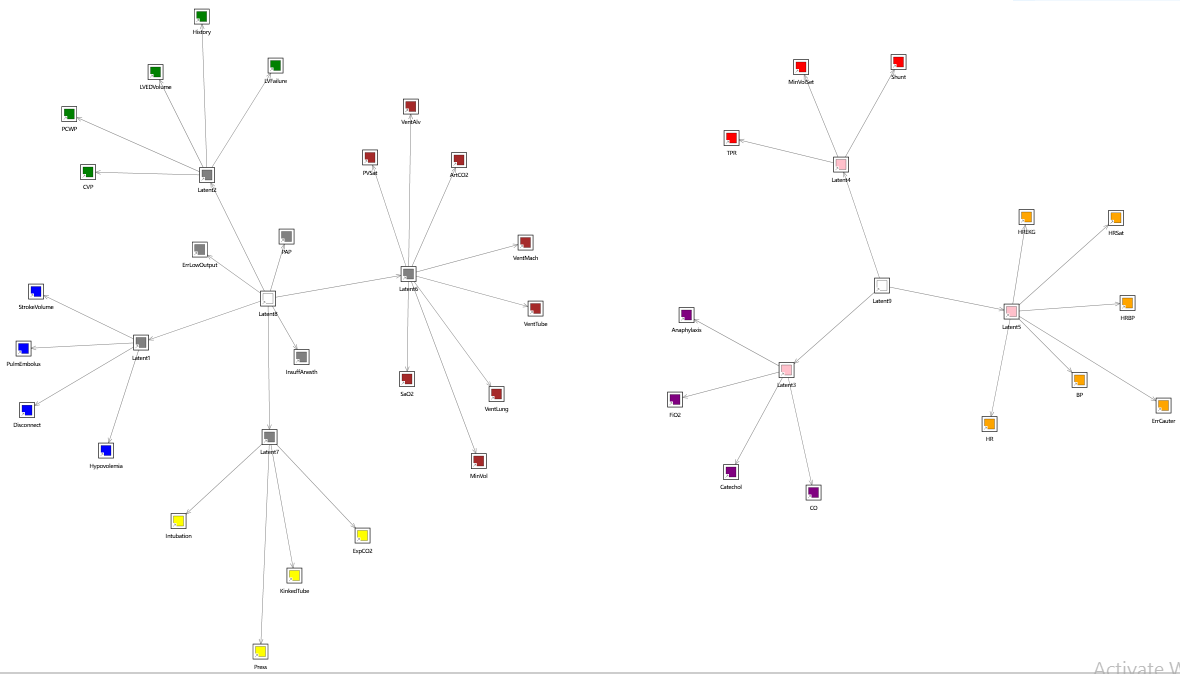
Hierarchical
(since version 7.20)
This algorithm, which is unique to Bayes Server, creates a hierarchy of nodes, built layer by layer. Each layer consists of a number of groups. Each group consists of similar variables as determined by the algorithm. Individual groups are connected via a parent discrete latent variable. Therefore the algorithm generates multiple latent variables, and latent variables themselves can be subsequently clustered in groups.
This algorithm currently supports the following:
- Discrete variables.
- Continuous variables.
- Hybrid networks with both discrete ad continuous variables.
- Learning with missing data.
An example output from the algorithm is shown below.
Chow-Liu algorithm
(since version 7.12)
Creates a Bayesian network which is a tree. The tree is constructed from a weighted spanning tree over a fully connected graph whose connections are weighted by a metric such as Mutual Information.
This algorithm currently supports the following:
- Discrete variables.
- Continuous variables.
- Learning with missing data.
References:
- Approximating discrete probability distributions with dependence trees | C Chow, C Liu - IEEE transactions on Information Theory, 1968
Root
An optional argument which determines the root of the generated tree.
TAN algorithm
(since version 7.12)
The Tree Augmented Naive Bayes algorithm (TAN) builds a Bayesian network that is focused on a particular target T (e.g. for classification). The algorithm creates a Chow-Liu tree, but using tests that are conditional on T (e.g. conditional mutual information). Then additional links are added from T to each node in the Chow-Liu tree.
This algorithm currently supports the following:
- Discrete variables.
- Continuous variables.
- Learning with missing data.
References
See the Chow-Liu algorithm.
Root
An optional argument which determines the root of the generated tree.
Target
Determines the target for the learning algorithm. For example, the node which you are trying to predict.
Chaining algorithms
Chaining of algorithms provides extra flexibility. For example you could start with a Chow-Liu tree which can be constructed very quickly. You may then wish to use the Search & Score algorithm to augment the tree with some more complex structure.
You could also start with a Search & Score, then use the Clustering algorithm.
When chaining, be sure to:
- Fully complete the wizard for each algorithm
- Include any links learned by the previous algorithm as link constraints when restarting the wizard.
Defining variables
In order to perform structural learning from a data set, you must have first defined your variables/nodes. If required, these can be automatically determined using the Add nodes from data feature.
Not all variables have to be mapped to data columns. Any variables that are not mapped are ignored during the learning process.
Link constraints
If required link constraints can be defined before learning. The different types of link constraint are documented in
BayesServer.Learning.Structure.LinkConstraintMethod in the Bayes Server API. The link constraint failure modes
are documented in BayesServer.Learning.Structure.LinkConstraintFailureMode in the Bayes Server API.