A latent variable, is a variable in a Bayesian network that is neither an input or output variable, and hence has no data associated with it during parameter learning.

Latent variables can either be discrete, or continuous.

Tip

Latent variables are also known as hidden variables.

Discrete latent variables

An example of a discrete latent variable is the Cluster node in the mixture model network shown below.

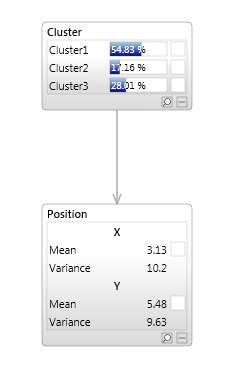
Position Mixture Model

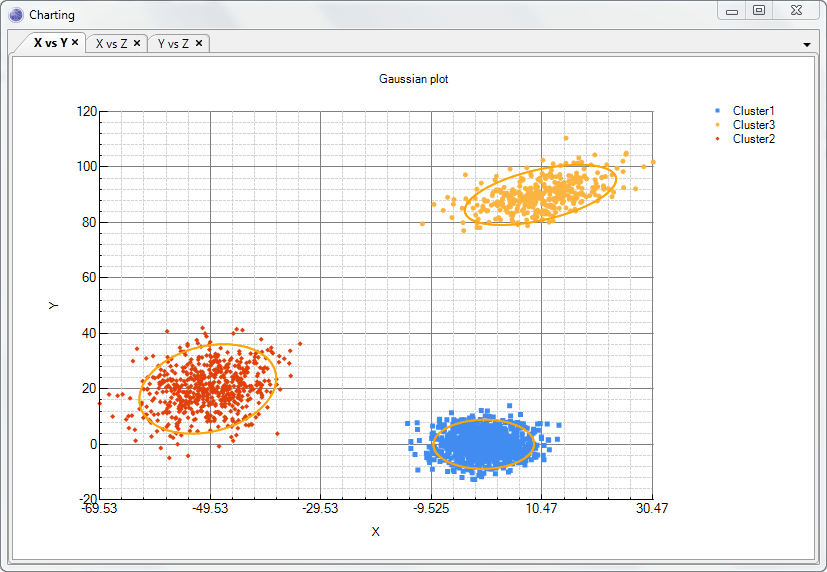
Instead of a single multivariate Gaussian, we have made the model more flexible by allowing multiple multivariate Gaussians, as shown in the image below.

Exercise Clustering Charting

Continuous latent variables

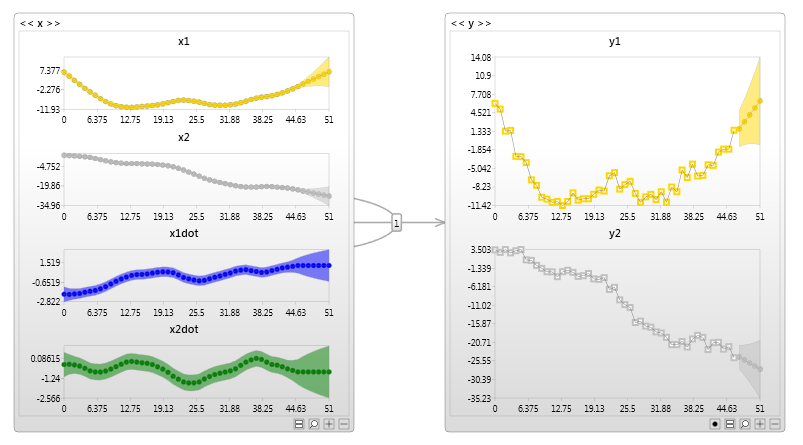
An example of a continuous latent variable is the x node in the Kalman filter network shown below.

The continuous latent variable is used in this case to represent an unobservable process.

Tip

Models such as this are often used to track missiles.

Kalman Filter
Tip

Continuous latent variables can also be used for dimensionality reduction (e.g. probabilistic PCA).